where
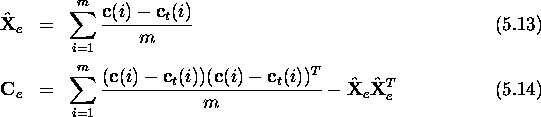
where m is the number of candidate landmarks in the tracked landmark.
We are seeking in this section a method for combining individual
estimates obtained from different tracked landmarks. This can be
accomplished using the merging operation defined above if we can
obtain an error model for estimates obtained from each tracked
landmark. An error model for a particular tracked landmark T can be
constructed using cross-validation. That is, we measure how
well each observed candidate landmark in T is predicted by the rest
of the candidate landmarks in T. This is a quantity which is fixed
for a given tracked landmark, and hence can be computed a
priori. More formally, for each landmark candidate ![]() which is a
member of a tracked landmark
which is a
member of a tracked landmark ![]() , we remove
, we remove
![]() from T to obtain T' and use T' to estimate the camera
position
from T to obtain T' and use T' to estimate the camera
position ![]() of
of ![]() , using the position estimation
method described in Section 1 of this chapter. The error model
E for T is then described as an AT with two components,
, using the position estimation
method described in Section 1 of this chapter. The error model
E for T is then described as an AT with two components,
![]() being the the average displacement of
being the the average displacement of ![]() from the true position
from the true position ![]() for all
for all ![]() of T, and
of T, and
![]() being the total covariance of the same displacements,
being the total covariance of the same displacements,
![]()
where
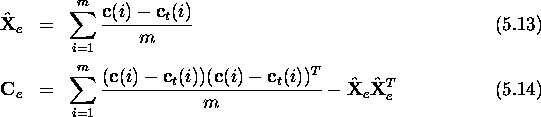
where m is the number of candidate landmarks in the tracked landmark.
Note that while the merging operation defined previously for combining
noisy estimates assumed zero mean error, it is possible for
![]() to be non-zero; a tracked landmark may, for whatever
reason, contain systematic error. In order to maintain our assumption
that the mean error is zero, we subtract this estimated systematic
error from the position estimates prior to merging.
to be non-zero; a tracked landmark may, for whatever
reason, contain systematic error. In order to maintain our assumption
that the mean error is zero, we subtract this estimated systematic
error from the position estimates prior to merging.